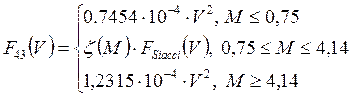Жаропонижающие средства для детей назначаются педиатром. Но бывают ситуации неотложной помощи при лихорадке, когда ребенку нужно дать лекарство немедленно. Тогда родители берут на себя ответственность и применяют жаропонижающие препараты. Что разрешено давать детям грудного возраста? Чем можно сбить температуру у детей постарше? Какие лекарства самые безопасные?
Инструкция
Найдите силу сопротивления движению, которая действует на равномерно прямолинейно движущееся тело. Для этого при помощи динамометра или другим способом измерьте силу, которую необходимо приложить к телу, чтобы оно двигалось равномерно и прямолинейно. По третьему закону Ньютона она будет численно равна силе сопротивления движения тела.
Определите силу сопротивления движению тела, которое перемещается по горизонтальной поверхности. В этом случае сила трения прямо пропорциональна силе реакции опоры, которая, в свою очередь равна силе тяжести, действующей на тело. Поэтому сила сопротивления движению в этом случае или сила трения Fтр равна произведению массы тела m, которая измеряется весами в килограммах, на ускорение свободного падения g≈9,8 м/с² и коэффициент пропорциональности μ, Fтр=μ∙m∙g. Число μ называется коэффициентом трения и зависит от поверхностей, входящих в контакт при движении. Например, для трения стали по дереву этот коэффициент равен 0,5.
Рассчитайте силу сопротивления движению тела, движущегося по наклонной плоскости . Кроме коэффициента трения μ, массы тела m и ускорения свободного падения g, она зависит от угла наклона плоскости к горизонту α. Чтобы найти силу сопротивления движению в этом случае, нужно найти произведения коэффициента трения, массы тела, ускорения свободного падения и косинуса угла, под которым плоскость наклонена к горизонту Fтр=μ∙m∙g∙сos(α).
При движении тела в воздухе на невысоких скоростях сила сопротивления движению Fс прямо пропорциональна скорости движения тела v, Fc=α∙v. Коэффициент α зависит от свойств тела и вязкости среды и рассчитывается отдельно. При движении на высоких скоростях, например, при падении тела со значительной высоты или движении автомобиля, сила сопротивления прямо пропорциональна квадрату скорости Fc=β∙v². Коэффициент β дополнительно рассчитывается для высоких скоростей.
Для определения силы сопротивления воздуха создайте условия, при которых тело начнет под действием силы тяжести двигаться равномерно и прямолинейно. Рассчитайте значение силы тяжести, оно будет равно силе сопротивления воздуха. Если тело движется в воздухе, набирая скорость, сила его сопротивления находится при помощи законов Ньютона, также силу сопротивления воздуха можно найти из закона сохранения механической энергии и специальных аэродинамических формул.
Вам понадобится
- дальномер, весы, спидометр или радар, линейка, секундомер.
Инструкция
Перед измерением сопротивления б/у резистора обязательно выпаяйте его из старой платы или блока. Иначе он может быть шунтирован другими деталями схемы, и вы получите неправильные показания его сопротивления .
Видео по теме
Чтобы найти электрическое сопротивление проводника, воспользуйтесь соответствующими формулами. Сопротивление участка цепи находится по закону Ома. Если же известен материал и геометрические размеры проводника, его сопротивление можно рассчитать при помощи специальной формулы.

Вам понадобится
- - тестер;
- - штангенциркуль;
- - линейка.
Инструкция
Вспомните, что подразумевает собой понятие резистора. В данном случае под резистором надо понимать любой проводник или элемент электрической цепи, имеющий активное резистивное сопротивление. Теперь важно задаться вопросом о том, как действует изменение значения сопротивления на значение силы тока и от чего оно зависит. Суть явления сопротивления заключается в том, что атомы вещества резистора формируют своего рода барьер для прохождения электрических зарядов. Чем выше сопротивление вещества, тем более плотно расположены атомы в решетке резистивного вещества. Данную закономерность и объясняет закон Ома для участка цепи. Как известно, закон Ома для участка цепи звучит следующим образом: сила тока на участке цепи прямо пропорциональна напряжению на участке и обратно пропорциональна сопротивлению самого участка цепи.
Изобразите на листе бумаги график зависимости силы тока от напряжения на резисторе, а также от его сопротивления, исходя из закона Ома. Вы получите график гиперболы в первом случае и график прямой во втором случае. Таким образом, сила тока будет тем больше, чем больше напряжение на резисторе и чем меньше сопротивление. Причем зависимость от сопротивления здесь более яркая, ибо она имеет вид гиперболы.
Обратите внимание, что сопротивление резистора также изменяется при изменении его температуры. Если нагревать резистивный элемент и наблюдать при этом за изменением силы тока, то можно заметить, как при увеличении температуры уменьшается сила тока. Данная закономерность объясняется тем, что при увеличении температуры увеличиваются колебания атомов в узлах кристаллической решетки резистора, уменьшая таким образом свободное пространство для прохождения заряженных частиц. Другой причиной, уменьшающей силу тока в данном случае, является тот факт, что при увеличении температуры вещества увеличивается хаотичное движение частиц, в том числе заряженных. Таким образом, движение свободных частиц в резисторе становится в большей степени хаотичным, чем направленным, что и сказывается на уменьшении силы тока.
Видео по теме
После ознакомления со свойствами воздуха рассмотрим движение в нём какого-либо тела. Для этого обратимся к наиболее простому случаю — действию потока на прямоугольную пластинку, поставленную перпендикулярно к нему. Например, возьмём большой лист фанеры и будем двигаться с ним или, наоборот, будем стоять, подставляя его действию ветра. Воздух будет давить на лист, препятствуя движению. Это противодействие воздуха телу принято называть сопротивлением тела или силой лобового сопротивления и обозначать через Q. Название «лобовое сопротивление» показывает, что эта сила действует навстречу телу и препятствует его движению, так как направлена прямо в «лоб». Возникновение лобового сопротивления в основном объясняется разностью давления перед телом и позади него ко повышенным давлением, которая заставляет набегающие струйки воздуха заранее расступаться перед телом (рис. 6).
Рис. 6. Перед телом струйки воздуха расступаются, образуя поджатые воздуха; позади тела струйки смыкаются, образуя разрежение и вихри.
Позади тела струйки не успевают смыкаться и там образуется область с несколько пониженным давлением, заполненная вихрями.
Величина лобового сопротивления зависит от площади наибольшего поперечного сечения тела, перпендикулярного потоку, иначе —от площади миделя S (рис. 7, а). Чем больше у листа фанеры, самолёта, автомобиля, снаряда миделевое сечение, часто называемое лобовой площадью, тем обычно больше сопротивление тела, так как при возрастании этой площади соответственно увеличивается число частиц воздуха, встречаемых телом, и, кроме того, изменяется характер обтекания тела.
Лобовое сопротивление в значительной степени зависит от скорости движения тела: чем больше скорость, тем большую массу набегающих частичек воздуха будет встречать тело в каждый момент времени, следовательно, тем затруднительнее ему двигаться.
Сопротивление тела, или лобовое сопротивление, зависит от плотности воздуха р, так как чем плотнее воздух, тем больше частиц воздуха находится в единице объёма и тем труднее в нём двигаться.
Кроме перечисленных выше факторов S, v, ρ, на величину сопротивления оказывает большое влияние форма тела. Например, если взять два тела с одинаковым миделем — веретенообразное тело и диск — и обдувать их, как показано на рис. 7, б, то можно убедиться, что веретенообразное тело обладает в 50-80 раз меньшим сопротивлением, чем диск.
![]()
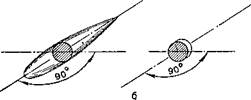
Рис. 7: а — площадь миделя различных тел; б — при одинаковых миделях сопротивление веретенообразного тела меньше, чем диска,
в 50-80раз.
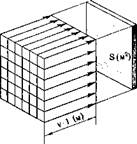
Рис. 8. Ньютон предположил, что весь объём набегающего воздуха останавливается пластинкой.
Мы установили, от каких причин зависит сопротивление тела, но практиков всегда интересует, как его подсчитать.
Ньютон следующим образом подошёл к количественному определению силы сопротивления тела в воздухе.
Рассмотрим случай набегания потока на плоскую прямоугольную пластину, поставленную перпендикулярно к потоку (рис. 8).
Набегающий на пластину воздух ею тормозится. Ньютон исходил из того предположения, что частицы воздуха, ударяясь о пластину, полностью теряют свою скорость. Тогда пластина за 1 сек остановит объём воздуха, равный объёму
прямоугольного параллелепипеда с основанием S м 2 и высотой v м, численно, равной скорости. Этот объём воздуха будет равен:
Следовательно, пластина за 1 сек остановит массу воздуха, равную:
Действующую на тело силу лобового сопротивления легко определить по второму закону Ньютона:
но Δt = 1 сек, a Δv = v, так как по предположению, скорость набегающего потока при соударении с пластинкой изменяется от v до нуля.
Следовательно, сила лобового сопротивления будет численно равна изменению количества движения набегающего потока.
Однако вывод формулы лобового сопротивления не совсем соответствует действительности, так как на самом деле частички воздуха при встрече с пластиной теряют скорость не полностью. Они огибают пластину, или, как принято говорить, обтекают её. В связи с этим в формулу Ньютона должен быть внесён некоторый поправочный коэффициент, который характеризовал бы интенсивность торможения потока.
Но подсчитать торможение потока пластиной или другим телом крайне трудно. Поэтому оно определяется опытным путём. Изготовленную модель тела в аэродинамической трубе обдувают воздухом и при помощи весов замеряют силу лобового сопротивления тела Q. Зная силу Q, плотность воздуха ρ, мидель модели S, скорость потока v и только что выведенную зависимость между ними, определяют поправочный коэффициент, который обозначается через С х.
![]()
Чем больше тормозится поток, тем больше коэффициент С х. Коэффициент С х получил название коэффициента лобового сопротивления тела. Он не постоянен и зависит от ряда причин. Для каждой модели тела, например для пластины, шара, веретенообразного тела, коэффициент С х имеет свои значения. Изменением этого коэффициента особенно интересуются при исследовании обтекания тел в аэродинамических трубах.
Для удобства пользования формулой лобового сопротивления перед ней ставится постоянный коэффициент 1 / 2 , и тогда она окончательно запишется в таком виде:
![]()
В этой формуле уже знакомая нам величина
легко замеряется при опыте, имеет размерность кГ/м 2 и называется скоростным напором.
Пользуясь формулой лобового сопротивления, можно решать многие задачи, например: определить, удержите ли вы против потока метровый лист фанеры, если будете с ним ехать на грузовом автомобиле со скоростью 40 км/час (или 11,1 м/сек), например, по Крестовому перевалу на Кавказе? Высота перевала 2382 м. В этой задаче площадь и скорость движения листа нам известны. Неизвестное — плотность на высоте 2382 м — возьмём из таблицы Международной стандартной атмосферы (ч. I, § 1), она будет ![]() ,неизвестный коэффициент лобового сопротивления возьмём из данных продувки пластин, С х =1,28. Подставляя эти значения в формулу лобового сопротивления, получим:
,неизвестный коэффициент лобового сопротивления возьмём из данных продувки пластин, С х =1,28. Подставляя эти значения в формулу лобового сопротивления, получим:
Можно самим определить, во сколько раз увеличится эта сила, если автомобиль будет ехать на той же скорости, но ниже — на высоте уровня моря.
Пользуясь той же формулой, интересно определить, при какой скорости вертикального потока воздуха парашютист, находящийся на высоте 1000 м, не сможет
спуститься на землю. Попробуем решить эту задачу, помня, что парашют имеет площадь купола, равную 60 м 2 . Коэффициент лобового сопротивления для такого купола Сx=0,7, плотность воздуха на высоте 1000 м.
![]()
Вес парашютиста с парашютом примем равным 88 кг.
Подставляя эти величины в формулу лобового сопротивления, получим:
![]()
Отсюда определится неизвестная вертикальная скорость восходящего потока:
![]()
Как видно, при скорости потока 6,1 м/сек сопротивление купола парашюта уравновесит вес парашютиста и парашюта, и спуск прекратится. А что, если вертикальная скорость потока станет чуть больше? Тогда парашютист, вместо того чтобы спускаться, будет подниматься вверх.
Такой редкий случай произошёл лет 25 назад в районе г. Сочи, когда парашютист, выпрыгнув с самолёта, попал в зону «воздушной болтанки», насыщенной мощными вертикальными потоками воздуха. К своему удивлению он не стал спускаться и, проболтавшись в воздухе около двух часов, наконец, приземлился.
В формуле лобового сопротивления коэффициент С х зависит от многих факторов: от формы тела, от ориентировки тела относительно потока, от состояния поверхности тела, от вязкости газа и других причин 1 .
Силы трения, возникающие при обтекании шероховатых тел, значительно больше, чем при обтекании гладких поверхностей. Вот почему поверхности у современных самолётов отделывают весьма тщательно. При этом сила трения сильно зависит от степени завихрённости обтекаемого потока. Незавихрённый плавный поток называют ламинарным или слоистым потоком. В ламинарном потоке частицы воздуха текут плавно, не смешиваясь между собой, не переходя из слоя в слой. Завихрённый поток принято называть турбулентным, он состоит из бесчисленного множества мелких вихрей. В турбулентном потоке происходит перемешивание частиц в направлении, перпендикулярном к потоку. При турбулентном движении воздуха тела испытывают большее трение, чем при ламинарном. Изучению турбулентного движения посвятил много выдающихся работ советский академик А. Н. Колмогоров.
Раз возникнув, в газе или в жидкости, вихри долго сохраняются в потоке и, увлекаемые общим течением, вытягиваются за телом в виде вихревой дорожки. Так, например, за давно прошедшим по реке пароходом на внешне спокойной глади ещё долго остаётся расходящийся след. Цвет этой дорожки отличен от другой части воды и свидетельствует о наличии в ней множества ещё незатухших вихрей, вызванных работой гребного винта и плохой обтекаемостью корпуса.
За летящим самолётом тоже остаётся след мелких и крупных вихрей. Парашютисты, прыгающие с самолётов, свидетельствуют о том, что, ещё не раскрывая парашюта и находясь значительно позади удаляющегося самолёта, они испытывают сильные толчки и вращательное движение тела, так называемую «болтанку».
Крупные воздушные вихри, срывающиеся на некоторых режимах полёта с крыла самолёта, могут быть опасными для хвостового оперения, особенно на больших скоростях полёта, где их действие можно сравнить с ударами кирпичей, срывающихся с крыла и летящих на хвостовое оперение.
В практике самолётостроения, лет 25 назад, бывали случаи, когда казалось бы проверенные серийные самолёты на некоторых режимах полёта начинали разваливаться в воздухе. Это происходило, как потом было установлено, из-за вибрации, вызванной срывом вихрей с крыла и попаданием их на неудачно расположенное хвостовое оперение. Это явление получило название баффтинг.
Лётчики-испытатели опытных самолётов хорошо знают «баффтинг» по тем характерным стукам и толчкам, которые к ним доходят в кабину через фюзеляж со стороны хвоста самолёта. Во избежание катастрофических последствий они должны немедленно перейти на другой режим полёта, снизив скорость самолёта.

Рис. 9. Воздух воздействует на тело в виде сил давления и сил трения.
Из знакомства с природой возникновения лобового сопротивления надо помнить, что при обтекании воздух воздействует на тело, в конечном счёте, в виде сил давления и сил трения (рис. 9). Других сил быть не может.
1 Когда скорость потока соизмерима со скоростью распространения звука, коэффициент С х начинает зависеть от скорости потока (см. ч. I, § 5)
При движении любого предмета по поверхности или в воздухе возникают силы, препятствующие этому. Их называют силами сопротивления или трения. В этой статье мы расскажем, как найти силу сопротивления, и рассмотрим факторы, влияющие на нее.
Для определения силы сопротивления необходимо воспользоваться третьим законом Ньютона. Эта величина численно равна силе, которую нужно приложить, чтобы заставить равномерно двигаться предмет по ровной горизонтальной поверхности. Это можно сделать при помощи динамометра. Сила сопротивления вычисляется по формуле F=μ*m*g. Согласно этой формуле, искомая величина прямо пропорциональна массе тела. Стоит учесть, что для правильного подсчета необходимо выбрать μ – коэффициент, зависящий от материала, из которого изготовлена опора. Принимают во внимание и материал предмета. Этот коэффициент выбирается по таблице. Для расчета используется постоянная g, которая равна 9,8 м/с2.




Сопротивление движения в воздухе используется во время прыжков с парашютом. В результате возникающего трения между куполом и воздухом скорость движения парашютиста снижается, что позволяет без ущерба для жизни заниматься парашютным спортом.
Введение
Разработка законов (функций) сопротивления воздуха имеет длительную историю. Этим занимались выдающиеся ученые и артиллеристы, и в результате проведения многочисленных полигонных стрельб были получены зависимости коэффициента лобового сопротивления от числа Маха, которые в сильной степени зависят от особенностей обтекания снаряда встречным потоком воздуха, т.е. главным образом от конфигурации головной части. Однако даже при наличии этой зависимости вычисление параметров траектории артиллерийского снаряда всегда представляла собой чрезвычайно сложную задачу, особенно если учитывать такие факторы, как кривизна поверхности и вращение Земли.
Для расчета траектории снаряда необходимо численно интегрировать систему дифференциальных уравнений внешней баллистики с помощью чрезвычайно трудоемкого метода конечных разностей, а в начале прошлого века в распоряжении вычислителей были только арифмометры и счеты. Для нового типа орудия требовались свои таблицы, составлять их приходилось годами, предварительно проведя полигонные стрельбы для определения параметров принятого закона сопротивления воздуха (главным образом, коэффициента формы снаряда). Известно, что первые внешнебаллистические расчеты немцы проводили, считая плотность воздуха постоянной и равной среднему значению в пределах высоты траектории.
Именно для быстрого составления баллистических таблиц по заказу армии США в Лаборатории баллистических исследований. в 1946 г. была создана первая вычислительная машина «Эниак» (ENIAC - Electronic Number Integrator And Computer - Электронный цифровой интегратор и вычислитель). Вычисления на «Эниаке» велись в десятичной системе, а для изменения программы требовалось установить в определенное положение тысячи переключателей и соединить сотни кабелей, и поэтому в среднем на подготовку машины к вычислению одной таблицы уходило два дня кропотливой ручной работы .
Таким образом, ускорение процесса вычисления параметров траектории всегда было актуальной задачей в ствольной, а затем и ракетной артиллерии. Для получения адекватных результатов необходимо соответствующее математическое описание закона сопротивления. Наиболее популярным в этом смысле длительное время являлся закон (функция) Сиаччи в виде эмпирической формулы, важным достоинством которой является непрерывная зависимость от скорости снаряда. Однако формула выведена применительно к устаревшим тупоголовым снарядам, использованным в качестве эталонных. После появления современных снарядов дальнобойной конфигурации были созданы новые законы сопротивления воздуха. Однако, в отличие от формулы Сиаччи, они заданы в дискретной (чаще всего в табличной) форме.
Наиболее распространенным в России (ранее - в СССР) законом сопротивления воздуха, используемым при расчете траекторий артиллерийских снарядов, является закон 1943 г. Однако до сих пор отсутствует представление этого закона в виде непрерывной зависимости от скорости снаряда, что затрудняет проведение расчетов на ЭВМ. В данной работе предлагается способ приведения закона Сиаччи к закону 1943 г. с помощью соответствующего коэффициента согласования в виде функции, непрерывно зависящей от скорости снаряда. Показано, что расхождение результатов расчета по предлагаемой аппроксимации с табличными данными не превышает допустимого с практической точки зрения.
Применение методики проиллюстрировано на конкретном примере.
1 Общая формула для силы сопротивления воздуха
На рисунке 1 показана схема сил, приложенных к снаряду на траектории: - сила тяжести; - равнодействующая аэродинамических сил, т.е. сила сопротивления воздуха. Она приложена в центре давления С , не совпадающем с центром массы O . Расстояние между этими точками определяется по формуле Гобара . На рисунке δ - угол атаки, т.е. угол между осью снаряда и касательной к траектории в данной точке (на касательной лежит вектор скорости снаряда ); - угол между вектором скорости и горизонтом. Если силу перенести в центр масс О и одновременно приложить к этой точке уравновешивающую силу (), то возникает пара сил, создающая опрокидывающий момент (его учитывают при исследовании движения снаряда как твердого тела). Силу , приложенную в центре масс, раскладывают на две составляющие: - сила лобового сопротивления (она лежит на касательной к траектории и направлена в сторону, обратную по отношению к вектору скорости) и - подъемная сила. В дальнейшем рассматриваем упрощенную схему приложения указанных сил, полагая и считая, что сила направлена по оси снаряда; в этом случае и .
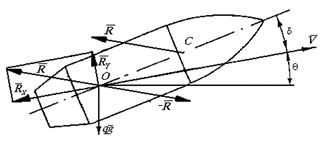
Рисунок 1 - Силы, приложенные к снаряду на траектории
Структуру фундаментального выражения для силы сопротивления воздуха получают с помощью теории подобия и размерностей, лежащей в основе методов физического моделирования:
|
где - плотность воздуха; - площадь миделевого сечения снаряда (d - калибр); - скоростной напор; - коэффициент лобового сопротивления; - число Маха; a - скорость звука в данной точке траектории; - число Рейнольдса; - кинематический коэффициент вязкости.
Зависимость определяют опытным путем для снарядов типовой («эталонной») формы. Подобие процессов обтекания снарядов воздушным потоком чаще всего не обеспечивается из-за различия конфигурации головной части, и, для того чтобы иметь возможность использовать имеющиеся опытные данные, вводят коэффициент формы снаряда
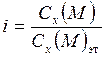 ,
,
учитывающий неполноту условий подобия. Данный коэффициент сравнительно слабо зависит от скорости снаряда, и его удобно использовать в качестве коэффициента согласования расчета по определению дальности стрельбы с опытом. В этом случае учитываются как форма снаряда, так и другие физические факторы, влияющие на движение снаряда.
Преобразуя формулу (1), получают выражение для «ускорения сопротивления воздуха»
где q - масса снаряда. Далее вводят функцию
где y - высота; - плотность воздуха на поверхности Земли в точке выстрела. Кроме того, для получения более удобных для практических расчетов значений соответствующих величин, вводят множитель
где кг/м 3 - плотность воздуха для нормальных артиллерийских условий. Тогда (2), с учетом (1), будет иметь вид
В этом выражении фигурирует баллистический коэффициент
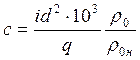 ..
..
Обычно принимают, что , т.е.
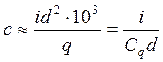 .
.
Здесь введен коэффициент относительной массы («поперечная нагрузка») , где d - в дециметрах. Видно, что баллистический коэффициент (а, следовательно, и сила сопротивления воздуха) изменяется обратно пропорционально калибру.
носит название закона сопротивления воздуха, так часто называют и зависимость . Опуская постоянный множитель в (4), можно записать пропорциональное соотношение
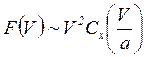 .
.
Как известно , скорость звука
где - показатель адиабаты для воздуха, обычно принимаемый равным 1,4; R
-
универсальная газовая постоянная; ![]() - «виртуальная» температура, учитывающая влажность воздуха; T
-
абсолютная температура; e
-
давление водяного пара; h
-
давление влажного воздуха/
- «виртуальная» температура, учитывающая влажность воздуха; T
-
абсолютная температура; e
-
давление водяного пара; h
-
давление влажного воздуха/
Эталонные законы сопротивления воздуха приведены к скорости звука в нормальных условиях ![]() м/с, поэтому аргумент преобразуют:
м/с, поэтому аргумент преобразуют:
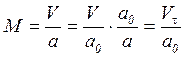 .
.
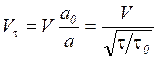 -
-
так называемая виртуальная скорость. Таким образом,
![]()
Соответственно,
|
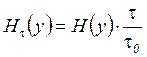 .
.
Зависимость обычно задают по :
Проведя довольно громоздкие вычисления, связанные с интегрированием соответствующих выражений, получим
|
2 Законы сопротивления воздуха
Л. Эйлер при решении задачи о полете снаряда пользовался функцией ![]() , установленной Ньютоном и применяемой в основном для дозвуковых скоростей. Одной из первой была степенная функция Маиевского-За-буд-ско-го
, установленной Ньютоном и применяемой в основном для дозвуковых скоростей. Одной из первой была степенная функция Маиевского-За-буд-ско-го
![]()
При составлении этой формулы в качестве эталонного был принят снаряд старой формы, имеющий короткую головную, длинные цилиндрическую и запоясную части. Коэффициенты выбирались так, чтобы на границах областей значения сопротивления были одинаковы, но при этом на графике появляются угловые точки, вследствие чего производные сопротивления по скорости терпят в этих точках конечные разрывы. Кроме того, при расчете траектории ее неудобно делить на ряд участков по скорости. В настоящее время на практике этот закон не используется.
Базируясь на работах Маиевского-Забудского и опытах конца XIX века, итальянский баллистик Франческо Сиаччи предложил новую функцию сопротивления воздуха , носящую его имя (1888 г.). Сиаччи также принял за эталонный снаряд старой формы, но сгладил угловые точки на графике . Большой заслугой Сиаччи является эмпирическая аппроксимация закона сопротивления воздуха в предложенной им форме (5) :
Этот закон многократно апробирован на практике и находит широкое применение при расчете траекторий, при соответствующем значении коэффициента формы. При малых скоростях закон Сиаччи близок к квадратичному, а при больших - к линейному.
С развитием артиллерии основным становится современный снаряд дальнобойной формы, имеющий удлиненную головную часть и сравнительно короткую хвостовую часть. Опыты по созданию новой функции проводились после Первой мировой войны в ряде стран, например, в 1921-1923 гг. во Франции (законы Гарнье и Дюпуи).
В нашей стране был создан закон сопротивления воздуха 1930 г. На его основе составлены таблицы внешней баллистики АНИИ, однако выяснилось, что данный закон дает неточные результаты при расчете траектории с большими начальными скоростями; кроме того, коэффициент формы современных снарядов по отношению к функции 1930 г. заметно колеблетсяпри различных скоростях.
3 Закон 1943 г.
Перед Великой Отечественной войной в СССР были начаты работы по установлению новой функции сопротивления воздуха на основе обработки результатов стрельб современными снарядами дальнобойной формы. Эти работы были закончены в 1943 г., новая функция получила название закон Артиллерийской академии им. Ф.Э. Дзержинского, или просто закон 1943 г. При этом. была обнаружена ошибка функции Сиаччи, проявляющаяся при скорости снаряда более 1410 м/с. Закон 1943 г. принят в нашей стране в качестве основного. Применительно к этой функции проводятся все баллистические расчеты, хотя ввиду наличия таблиц находят применение также функции 1930 г. и Сиаччи.
Полная таблица закона 1943 г. содержится в книге ; в сокращенном виде она приведена в , наряду с законами Сиаччи и 1930 г. В функция 1943 г. задана в пределах ограниченного диапазона (), разбитого на участки:
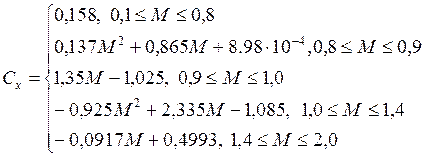
В имеется следующее описание закона 1943 г.:
Таблица 1 - Переходный множитель
Скорость, м/с | М | Переходный множитель |
0…150 | 0…0,44 | 0,61 |
150…250 | 0,44…0,733 | 0,58 |
250…300 | 0.733…0,880 | 0,48 |
300…341 | 0,880…1,0 | 0.60 |
341…400 | 1,0…1,173 | 0,57 |
400…500 | 1,173…1,466 | 0,50 |
500…700 | 1,466…2,053 | 0,45 |
700…1000 | 2,053…2,932 | 0,48 |
Видно, что переходный множитель заметно зависит от скорости, так что усреднение его в пределах того или иного диапазона скоростей может привести к ошибкам расчета в другом диапазоне.
Коэффициенты формы для современных снарядов (ОФ) по отношению к закону 1943 г. изменяются в пределах , а по отношению к функции Сиаччи .
Таким образом, известные способы описания закона 1943 г. задают его дискретно (по точкам или по поддиапазонам), эмпирического описания в виде единой непрерывной функции скорости в пределах всего диапазона изменения числа Маха, подобного закону Сиаччи, закон не имеет. Дискретность описания закона 1943 г. неудобна при вычислении траекторий на ЭВМ, в связи с чем его пытаются выражать через закон Сиаччи, вводя корректирующий переходный множитель, однако и этот множитель задан дискретно. Поэтому на практике часто предпочитают использовать именно закон Сиаччи, но при некотором коэффициенте формы i , определяемом по известным условиям стрельбы.
4 Аппроксимация закона 1943 г.
Можно предложить такой способ коррекции закона Сиаччи и приведения его к закону 1943 г. . Определив по табличным данным (дискретную) зависимость коэффициента формы от скорости, затем аппроксимировать ее как некую непрерывную функцию скорости и затем производить пересчет следующим образом:
Результаты реализации этой идеи в среде пакета MathCAD
представлены на рисунке 2, где 1 - ; 2 - табличный закон 1943 г, ; 3 - функция согласования ![]() ; 4- аппроксимация функции согласования ; 5 -
; 4- аппроксимация функции согласования ; 5 - ![]() .
.
Функция согласования аппроксимируется полиномом 3-го порядка:
коэффициенты которого определены с помощью функции MathCAD linfit , относящейся к линейной комбинации аппроксимирующих формул:
; ![]() ;
; ![]() ;
; ![]() .
.
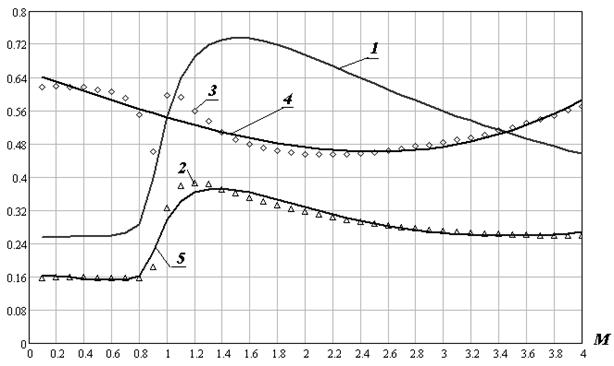
Рисунок 2 - Аппроксимация закона 1943 г.:
Из рисунка 2 видно, что аппроксимирующая кривая ![]() в целом достаточно близка к табличной зависимости, за исключением участка в районе максимума, однако это не должно привести к существенной ошибке, особенно при высоких скоростях снаряда ().
в целом достаточно близка к табличной зависимости, за исключением участка в районе максимума, однако это не должно привести к существенной ошибке, особенно при высоких скоростях снаряда ().
Таким образом, принимаем следующее эмпирическое описание закона 1943 г.:
|
В таблице 2 дано сравнение данных, приведенных в работе , с получаемыми по предлагаемой аппроксимации: 1 - табличные значения ; 2 - расчет по данной методике; 3 - отклонение, %.
Таблица 2 - Сравнение аппроксимирующих и табличных значений
M | |||
0,158 | 0,1 576 | 0,25 |
|
0,158 | 0,15 77 | 0,19 |
|
0,157 | 0.15 70 | ||
0,160 | 0.1 57 | 1,88 |
|
0,335 | 0. 3454 | 3,10 |
|
0,385 | 0.3 87 | 0,52 |
|
0,378 | 0.37 6 | 1,31 |
|
0,351 | 0.3 556 | 1 ,3 1 |
|
0,332 | 0.3 344 | 0,72 |
|
0,316 | 0.3 161 | 0 ,03 |
|
0,287 | 0.28 42 | 0,98 |
|
0,270 | 0.26 68 | 1 , 18 |
|
0,261 | 0.25 93 | 0 , 65 |
|
0,260 | 0.2 575 | 0,96 |
Видно, что отличие результатов расчета по аппроксимации от табличных значений с практической точки зрения вполне допустимо.
5 Пример расчета
Применение предложенной аппроксимации проиллюстрируем на примере расчета параметров траектории снаряда линкора «Бисмарк», который был проведен автором при математическом моделировании обстрела английского линейного крейсера «Худ» 24 мая 1941 г. Подробное описание «дуэли» двух выдающихся кораблей приведено в .
В работе читаем: «…коэффициент формы i
следует рассматривать как параметр, позволяющий согласовывать результаты теоретических расчетов с опытными данными. Например, пусть на основании стрельб снарядами определенного типа при фиксированных значениях начальной скорости и угла бросания найдена опытная дальность стрельбы Х.
…По величинам Х
, и можно определить коэффициент формы снаряда i
. Если расчет траектории проводить с использованием коэффициента , удовлетворяющего выражению ![]() при тех же значениях и , то получим дальность стрельбы, совпадающую с опытной. Этот способ применяется для определения коэффициента формы при составлении таблиц стрельбы для конкретного орудия».
при тех же значениях и , то получим дальность стрельбы, совпадающую с опытной. Этот способ применяется для определения коэффициента формы при составлении таблиц стрельбы для конкретного орудия».
Соответствующие вычисления проводят, используя известную систему уравнений, описывающих движение снаряда как материальной точки :
где - угол наклона касательной к траектории (вектора скорости) относительно горизонта.
Именно так был определен коэффициент i для снарядов «Бисмарка», На линкоре были установлены восемь 380-мм орудий (по два в каждой из четырех башен) 38cm /52 SK C /34. Известно, что максимальная дальность 35 550 м достигается при массе снаряда 800 кг, дульной скорости 820 м/с и угле возвышения . Методом подбора, пользуясь соответствующей программой численного решения системы (9), было определено и .
В работе приведены параметры траектории при стрельбе с различными углами возвышения; в таблице 3 дается сравнение этих данных с результатами расчета, полученными с помощью закона Сиаччи при (в знаменателе). Расхождение между этими данными составляет единицы и доли процента. Закон Сиаччи был использован, поскольку расчеты, проведенные немцами, могли быть получены только с помощью именно этого закона. Это подтверждается сведениями в статье , в которой представлены результаты расчетов внешней баллистики «Бисмарка», выполненные в 1939-1940 гг. во время достройки линкора на судоверфи «Блом и Фосс» . Данные результаты также представлены и в графической форме на Интернет-сайте линейного крейсера «Худ» .
Таблица 3 - Сравнение данных с результатами расчета по предлагаемой методике
Угол возвышения, град | Дальность стрельбы, м | Угол падения снаряда, град | Время в полете, с | Скорость падения снаряда, м/с |
|
5000 / 4 860 | 2,4 / - 2,38 | 6,5 / 6,29 | 727 / 729,4 |
||
10000 / 9 900 | 5,8 / - 5,75 | 13,9 / 13.68 | 641 / 644,2 |
||
15000 / 14 880 | 10,4 / - 10,27 | 22,3 / 22,03 | 568 / 572,7 |
||
12,1 | 20000 / 20 040 | 16,4 / -16,37 | 32,0 /31,92 | 511 / 516,2 |
|
16,8 | 25000 / 25 090 | 23,8 / - 23,62 | 43,0 / 42,92 | 473 / 481,3 |
|
22,4 | 30000 / 30 120 | 31,9 / - 31,62 | 55,5 / 55,34 | 457 / 467,4 |
|
29,1 | 0,97 | 527 ,7 | 13 ,9 | 27 ,89 |
|
Данные [ 14] |
Расхождение между требуемыми значениями угла возвышения , а также конечными параметрами траектории невелико. Ближе всего к немецким данным результаты расчета по закону Сиаччи, что свидетельствует об использовании именно этого закона. Коэффициент формы для закона 1943 г. несколько меньше единицы, т.е. снаряды «Бисмарка» имели «более дальнобойную» форму по сравнению с эталонными снарядами, использованными при получении закона 1943 г.
Заключение
Основные результаты работы сводятся к следующему.
1) Рассмотрена возможность приведения закона сопротивления воздуха 1943 г., принятого в России как основного при расчете траекторий артиллерийских снарядов, к закону Сиаччи. Достоинством последнего является непрерывная зависимость от скорости снаряда, однако данный закон получен для устаревших, тупоголовых снарядов и не может быть непосредственно использован при расчете современных, т.е. дальнобойных, снарядов.
2) Корректирующий множитель предложен в виде аналитической аппроксимации последовательности дискретных коэффициентов согласования, представляющей собой непрерывную функцию числа Маха. Благодаря применению предлагаемой аппроксимации упрощается вычисление параметров траектории на ЭВМ.
3) Показано, что отличие результатов расчета по предложенной методике от табличных значений не превышает допустимое с практической точки зрения.
4) Приведен пример использования предложенной аппроксимации.
Список литературы
1. Ефремов А.К. Реконструкция проектирования сверхдальнобойного орудия - «Парижской пушки» // Известия РАРАН. 2010. Вып.3(65). С. 105-116.
2. Дмитриевский А.А., Лысенко Л.Н. Внешняя баллистика: учеб. для вузов. 4-е изд. М.: Машиностроение, 2005. 608с.
3. Вентцель Д.А., Окунев Б.Н., Шапиро Я.М. Внешняя баллистика. Ч. I . Л.: Арт. акад. им. Ф.Э.Дзержинского, 1933.
4. Шапиро Я.М. Внешняя баллистика. М.: Оборонгиз, 1946.
5. Гантмахер Ф.Р., Левин М.А. Теория полета неуправляемых ракет. М.: Физматгиз, 1959. 360с.
6. Правдин В.М., Шанин А.П. Баллистика неуправляемых летательных аппаратов. Снежинск: Изд-во РФЯЦ-ВНИИТФ, 1999. 496с.
7. Ефремов А.К. Автономные информационные и управляющие системы. В 4 т. Т. 4 / Под ред. А.Б. Борзова. М.: ООО НИЦ «Инженер», ООО «Онико-М», 2011. 330 с.
8. Мюлленгейм-Рехберг Б.Б., фон. Линкор «Бисмарк»: пер. с англ. / под ред. А.К. Ефремова. М.: Эксмо, 2006.
9. Баллистика ствольных систем / РАРАН; под ред. Л.Н. Лысенко и А.М. Липанова. М.: Машиностроение, 2006.
10. Campbell J. Naval Weapons of World War Two. London: Conway Maritime Press, 2002.
11. Jurens W.J. The Loss of HMS Hood - a Re-Examination // Warship International. 1987. Vol. 24, no 2. P. 122-180.
12. Obercommando der Kriegsmarine, Unterlagen und Richtlinien zur Bestimmung der Hauptkampfentfernung und der Geschoswahl. Berlin. 1940.
При реальных физических движениях тел в газовой или жидкостной среде трение накладывает огромный отпечаток на характер движения. Каждый понимает, что предмет, сброшенный с большой высоты (например, парашютист, прыгнувший с самолета), вовсе не движется равноускоренно, так как по мере набора скорости возрастает сила сопротивления среды. Даже эту. относительно несложную, задачу нельзя решить средствами «школьной» физики; таких задач, представляющих практический интерес, очень много. Прежде чем приступать к обсуждению соответствующих моделей, вспомним, что известно о силе сопротивления.
Закономерности, обсуждаемые ниже, носят эмпирический характер и отнюдь не имеют столь строгой и четкой формулировки, как второй закон Ньютона. О силе сопротивления среды движущемуся телу известно, что она, вообще говоря, растет с ростом скорости (хотя это утверждение не является абсолютным). При относительно малых скоростях величина силы сопротивления пропорциональна скорости и имеет место соотношение F co п p = k 1 v, где k 1 определяется свойствами среды и формой тела. Например, для шарика k 1 = 6πμr - это формула Стокса, где μ -динамическая вязкость среды, r - радиус шарика. Так, для воздуха при t = 20°С и давлении 1 атм.μ = 0,0182 Н∙с∙м -2 , для воды 1,002 Н∙с∙м -2 , для глицерина 1480 Н∙с∙м -2 .
Оценим, при какой скорости для падающего вертикально шара сила сопротивления сравняется с силой тяжести (и движение станет равномерным).
![]()
Пусть r = 0,1 м, ρ = 0,8∙10 3 кг/м 3 (дерево). При падении в воздухе v* ≈ 960 м/с, в воде v *≈ 17 м/с, в глицерине v* ≈ 0,012 м/с.
На самом деле первые два результата совершенно не соответствуют действительности. Дело в том, что уже при гораздо меньших скоростях сила сопротивления становится пропорциональной квадрату скорости: F co п p = k 2 v 2 . Разумеется, линейная по скорости часть силы сопротивления формально также сохранится, но если k 2 v 2 >> k 1 v, то вкладом k 1 v можно пренебречь (это конкретный пример ранжирования факторов). О величине k 2 известно следующее: она пропорциональна площади сечения тела S, поперечного по отношению к потоку, и плотности среды ρ среды и зависит от формы тела. Обычно представляют k 2 = 0,5сSρ срeды, где с - коэффициент лобового сопротивления - безразмерен. Некоторые значения с (для не очень больших скоростей) приведены на рис. 7.6.
При достижении достаточно большой скорости, когда образующиеся за обтекаемым телом вихри газа или жидкости начинают интенсивно отрываться от тела, значение с в несколько раз уменьшается; для шара оно становится приблизительно равным 0,1. Подробности можно найти в специальной литературе.
Вернемся к указанной выше оценке, исходя из квадратичнойзависимости силысопротивления от скорости.
![]()
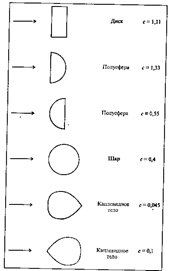
Рис. 7.6. Значения коэффициента лобового сопротивления для некоторых тел, поперечное сечение которых имеет указанную на рисунке форму (см. книгу П.А.Стрелкова)
Для шарика
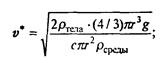 (7.5)
(7.5)
Примем r = 0,1 м, ρ = 0,8∙10 3 кг/м 3 (дерево). Тогда для движения в воздухе (ρ возд = 1,29 кг/м 3) получаем v* ≈ 18 м/с, в воде (ρ воды ≈ 1∙10 3 кг/м 3) v* ≈ 0,65 м/с, в глицерине (ρ глицерина = 1,26∙10 3 кг/м 3) v * ≈ 0,58 м/с.
Сравнивая с приведенными выше оценками линейной части силы сопротивления, видим, что для движения в воздухе и в воде ее квадратичная часть сделает движение равномерным задолго до того, как это могла бы сделать линейная часть, а для очень вязкого глицерина справедливо обратное утверждение. Рассмотрим свободное падение с учетом сопротивления среды. Математическая модель движения - уравнение второго закона Ньютона с учетом двух сил, действующих на тело; силы тяжести и силы сопротивления среды:
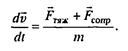 (7.6)
(7.6)
Движение является одномерным; проецируя векторное уравнение на ось, направленную вертикально вниз, получаем
![]() (7.7)
(7.7)
Вопрос, который мы будем обсуждать на первом этапе, таков: каков характер изменения скорости со временем, если все параметры, входящие в уравнение (7.7), заданы? При такой постановке модель носит сугубо дескриптивный характер. Из соображений здравого смысла ясно, что при наличии сопротивления, растущего со скоростью, в какой-то момент сила сопротивления сравняется с силой тяжести, после чего скорость больше возрастать не будет. Начиная с этого момента, dv/dt = 0, и соответствующую установившуюся скорость можно найти из условия mg – k 1 v – k 2 v 2 = 0 , решая не дифференциальное, а квадратное уравнение. Имеем
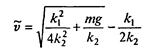 (7.8)
(7.8)
(второй - отрицательный - корень, естественно, отбрасываем). Итак, характер движения качественно таков: скорость при падении возрастает от v 0 до ; как и по какому закону - это можно узнать, лишь решив дифференциальное уравнение (7.7).
Однако, даже в столь простой задаче мы пришли к дифференциальному уравнению, которое не относится ни к одному из стандартных типов, выделяемых в учебниках по дифференциальным уравнениям, допускающих очевидным образом аналитическое решение. II хотя это не доказывает невозможность его аналитического решения путем хитроумных подстановок, но они не очевидны (один из лучших помощников в их поиске - справочник Камке). Допустим, однако, что нам удастся найти такое решение, выраженное через суперпозицию нескольких алгебраических и трансцендентных функций - а как найти закон изменения во времени перемещения? - Формальный ответ прост:
![]() (7.9)
(7.9)
но шансы на реализацию этой квадратуры уже совсем невелики. Дело в том, что класс привычных нам элементарных функций очень узок, и совершенно стандартна ситуация, когда интеграл от суперпозиции элементарных функций не может быть выражен через элементарные функции в принципе. Математики давно расширили множество функций, с которыми можно работать почти так же просто, как с элементарными (т.е. находить значения, различные асимптотики, строить графики, дифференцировать, интегрировать). Тем, кто знаком с функциями Бесселя, Лежандра, интегральными функциями и еще двумя десятками других, так называемых, специальных функций, легче находить аналитические решения задач моделирования, опирающихся на аппарат дифференциальных уравнений. Однако даже получение результата в виде формулы не снимает проблемы представления его в виде, максимально доступном для понимания, чувственного восприятия, ибо мало кто может, имея формулу, в которой сопряжены логарифмы, степени, корни, синусы и тем более специальные функции, детально представить себе описываемый ею процесс -а именно это есть цель моделирования.
В достижении этой цели компьютер - незаменимый помощник. Независимо от того, какой будет процедура получения решения - аналитической или численной, -задумаемся об удобных способах представления результатов. Разумеется, колонки чисел, которых проще всего добиться от компьютера (что при табулировании формулы, найденной аналитически, что в результате численного решения дифференциального уравнения), необходимы; следует лишь решить, в какой форме и размерах они удобны для восприятия. Слишком много чисел в колонке быть не должно, их трудно будет воспринимать, поэтому шаг, с которым заполняется таблица, вообще говоря, гораздо больше шага, с которым решается дифференциальное уравнение в случае численного интегрирования, т.е. далеко не все значения v и S, найденные компьютером, следует записывать в результирующую таблицу (табл. 7.2).
Таблица 7.2
Зависимость перемещения и скорости падения «безпарашютиста» от времени (от 0 до 15 с)
| t(c) | s(m) | v (м/с) | t(с) | S(м) | v (м/с) |
| 0 | 200,1 | 35,6 | |||
| 4,8 | 9,6 | 235,9 | 36,0 | ||
| 18,7 | 17,9 | 272,1 | 36,3 | ||
| 40,1 | 24,4 | 308,5 | 36,4 | ||
| 66,9 | 28,9 | 345,0 | 36,5 | ||
| 97,4 | 31,9 | 381,5 | 36,6 | ||
| 130,3 | 33,8 | 418.1 | 36,6 | ||
| 164,7 | 35,0 | 454,7 | 36,6 |
Кроме таблицы необходимы графики зависимостей v(t) и S(t); по ним хорошо видно, как меняются со временем скорость и перемещение, т.е. приходит качественноепонимание процесса.
Еще один элемент наглядности может внести изображение падающего тела через равные промежутки времени. Ясно, что при стабилизации скорости расстояния между изображениями станут равными. Можно прибегнуть и к цветовой раскраске - приему научной графики, описанному выше.
Наконец, можно запрограммировать звуковые сигналы, которые подаются через каждый фиксированный отрезок пути, пройденный телом - скажем, через каждый метр или каждые 100 метров - смотря по конкретным обстоятельствам. Надо выбрать интервал так, чтобы вначале сигналы были редкими, а потом, с ростом скорости, сигнал слышался все чаще, пока промежутки не сравняются. Таким образом, восприятию помогают элементы мультимедиа. Поле для фантазии здесь велико.
Приведем конкретный пример решения задачи о свободно падающем теле. Герой знаменитого фильма «Небесный тихоход» майор Булочкин, упав с высоты 6000 м в реку без парашюта, не только остался жив, но даже смог снова летать. Попробуем понять, возможно ли такое на самом деле или же подобное случается только в кино. Учитывая сказанное выше о математическом характере задачи, выберем путь численного моделирования. Итак, математическая модель выражается системой дифференциальных уравнений
![]() (7.10)
(7.10)
Разумеется, это не только абстрактное выражение обсуждаемой физической ситуации, но и сильно идеализированное, т.е. ранжирование факторов перед построением математической модели произведено. Обсудим, нельзя ли произвести дополнительное ранжирование уже в рамках самой математической модели с учетом конкретно решаемой задачи, а именно - будет ли влиять на полет парашютиста линейная часть силы сопротивления и стоит ли ее учитывать при моделировании.
Так как постановка задачи должна быть конкретной, мы примем соглашение, каким образом падает человек. Он - опытный летчик и наверняка совершал раньше прыжки с парашютом, поэтому, стремясь уменьшить скорость, он падает не «солдатиком», а лицом вниз, «лежа», раскинув руки в стороны. Рост человека возьмем средний - 1,7 м, а полуобхват грудной клетки выберем в качестве характерного расстояния - это приблизительно 0,4 м. Для оценки порядка величины линейной составляющей силы сопротивления воспользуемся формулой Стокса. Для оценки квадратичной составляющей силы сопротивления мы должны определиться со значениями коэффициента лобового сопротивления и площадью тела. Выберем в качестве коэффициента число с = 1,2 как среднее между коэффициентами для диска и для полусферы (выбор для качественной оценки правдоподобен). Оценим площадь: S = 1,7∙0,4=0,7 (м 2).
Выясним, при какой скорости сравняются линейная и квадратичная составляющие силы сопротивления. Обозначим эту скорость v**. Тогда
![]()
![]()
Ясно, что практически с самого начала скорость падения майора Булочкина гораздо больше, и поэтому линейной составляющей силы сопротивления можно пренебречь, оставив лишь квадратичную составляющую.
После оценки всех параметров можно приступить к численному решению задачи. При этом следует воспользоваться любым из известных численных методов интегрирования систем обыкновенных дифференциальных уравнений: методом Эйлера, одним из методов группы Рунге - Кутта, одним из многочисленных неявных методов. Разумеется, у них разная устойчивость, эффективность и т.д. - эти сугубо математические проблемы здесь не обсуждаются. Программа, реализующая метод Рунге - Кутта четвертого порядка, может быть взята из примера, приведенного в следующем параграфе или из какого-нибудь стандартного пакета математических программ.
Отметим, что существует немало программ, моделирующих простые физические процессы типа рассматриваемого. У них реализован, в той или иной мере профессионально, диалоговый интерфейс, позволяющий вводить параметры, получать на экране таблицы, графики, движущиеся изображения. Однако в них, как правило, остаются скрытыми физические законы, определяющие процесс, ограничения модели, возможности ее усовершенствования. Такие программы полезны скорее как сугубо иллюстративные.
Вычисления производились до тех пор, пока «безпарашютист» не опустилсяна воду. Примерно через 15 с после начала полета скорость стала постоянной и оставалась такой до приземления (рис. 7.7). Отметим, что в рассматриваемой ситуации сопротивление воздуха радикально меняет характер движения; при отказе от его учета график скорости, изображенный на рисунке, заменился бы касательной к нему в начале координат.
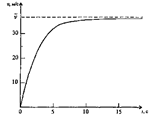
Рис. 7.7. График зависимости скорости падения «безпарашютиста» от времени
В некоторых случаях для ускорения процесса работы над какой-либо задачей целесообразно вместо составления программы воспользоваться готовой прикладной программой (например, табличным процессором). Покажем это на примере рассматриваемой задачи. В табл. 7.3 представлен небольшой фрагмент из табличного процессора Excel. Решение находится с помощью, так называемого, исправленного метода Эйлера - одного из возможных вариантов метода Рунге - Кутта второго порядка.
Кроме того, в ячейках D2, D4, D6 в таблице будем хранить соответственно значения шага вычислений, массы «безпарашютиста», величины mg . Это связано с тем, что все константы также удобно хранить в отдельных ячейках, чтобы в случае их изменения не пришлось переписывать расчетные формулы. Достаточно записать
Таблица 7.3
Фрагмент таблицы, где представлено решение задачи о «безпарашютнсте»
| А | В | |
| t | v | |
| 0 | ||
| =СУММ(АЗ; D2) | =B3+D2/2* ((D6-D8*B3^2) /D4+(D6-D8*(B3+D2*(D6-D8*B3^2)/D4)^2)/D4) | |
| =СУММ(А4; D2) | =B4+D2/2* ((D6-D8*B4^2) /D4+(D6-D8* (B4+D2* (D6- D8*B4^2)/D4)^2)/D4) | |
| =СУММ(А5; D2) | =B5+D2/2*((D6-D8*B5^2)/D4+(D6-D8*(B5+D2*(D6-D8*B5^2)/D4)^2)/D4) | |
| =СУМM(А6; D2) | =B6+D2/2* ((D6-D8*B6^2) /D4+ (D6-D8* (B6+D2* (D6-D8*B6^2)/D4)^2)/D4) | |
| =СУММ(А7; D2) | =B7+D2/2*((D6-D8*B7^2)/D4+(D6-D8*(B7+D2*(D6-D8*B7^2)/D4)^2)/D4) |
формулу правильно один раз, а затем скопировать в остальные ячейки, при этом, как известно, она «настраивается» на соответствующую ячейку.
Таблица 7.4
Конец работы -
Эта тема принадлежит разделу:
Моделирование как метод научного познания
Линейное программирование математическая дисциплина посвящ нная теории и методам решения экстремальных задач на множествах мерного векторного... Линейное программирование является частным случаем выпуклого программирования... Многие свойства задач линейного программирования можно интерпретировать также как свойства многогранников и таким...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ:
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:

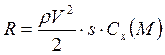 ,
,